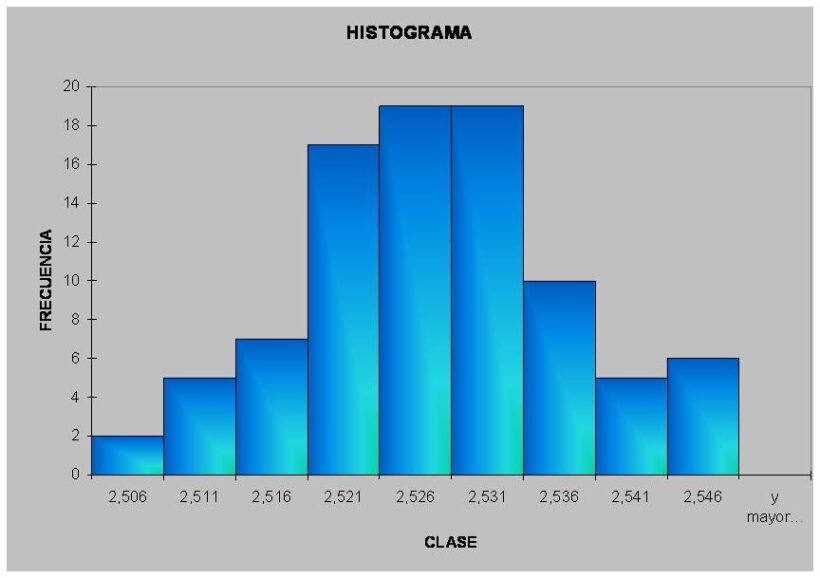
Un histograma es una representación gráfica que permite visualizar la distribución de un conjunto de datos numéricos. A diferencia de otros gráficos, como los de barras, el histograma muestra cómo se agrupan los valores en intervalos o rangos, llamados clases. Cada barra refleja la frecuencia con la que aparecen los datos dentro de esos intervalos.
Gracias a esta estructura, los histogramas ayudan a comprender patrones, concentraciones, dispersiones y tendencias en grandes volúmenes de información. Por ello, se utilizan ampliamente en campos como la estadística, la ingeniería, la economía y la ciencia de datos.
Características principales del histograma
El histograma combina sencillez visual con profundidad analítica. Aunque su diseño parece simple, cada elemento tiene un propósito definido.
Ejes y barras
El eje horizontal representa los intervalos de valores o clases. Por ejemplo, si se analizan las edades de un grupo de personas, los intervalos podrían ser de 0 a 10, de 11 a 20, y así sucesivamente. El eje vertical, en cambio, muestra la frecuencia, es decir, el número de datos que se encuentran dentro de cada intervalo.
Las barras de un histograma siempre están unidas, lo que indica la continuidad de los datos. Esta característica lo diferencia del gráfico de barras, donde las columnas se separan porque representan categorías independientes.
Frecuencia y densidad
En un histograma, la altura de cada barra refleja la frecuencia absoluta o relativa. La frecuencia absoluta indica cuántos valores caen dentro de un intervalo, mientras que la relativa muestra el porcentaje que representan sobre el total de los datos.
En algunos casos, especialmente cuando los intervalos no son iguales, se utiliza la densidad de frecuencia. Esta técnica ajusta la altura de las barras para mantener la proporcionalidad y asegurar una interpretación correcta.
Cómo se construye un histograma paso a paso
Crear un histograma es un proceso sencillo, aunque requiere organización y claridad en los datos. A continuación, se describe el procedimiento básico.
1. Recolección de datos
El primer paso consiste en reunir los datos numéricos que se van a analizar. Estos deben ser cuantitativos, ya que el histograma no puede representar categorías o cualidades, sino solo valores medibles.
2. Determinar el rango y los intervalos
Luego, se calcula el rango de los datos, es decir, la diferencia entre el valor máximo y el mínimo. Con base en ese rango, se decide cuántos intervalos o clases se utilizarán. Aunque no existe una regla exacta, es recomendable usar entre 5 y 15 intervalos para mantener la claridad visual.
3. Contar las frecuencias
Después, se contabiliza cuántos datos se encuentran dentro de cada intervalo. Este conteo formará la base del histograma y permitirá determinar la altura de las barras.
4. Dibujar el gráfico
Por último, se representan los intervalos en el eje horizontal y las frecuencias en el eje vertical. Cada barra se dibuja contigua a la anterior, lo que muestra la continuidad de los valores.
Interpretación del histograma
Analizar un histograma permite identificar patrones que revelan información valiosa sobre los datos. Dependiendo de la forma de las barras, es posible conocer si los valores se concentran, se dispersan o presentan sesgos.
Distribución simétrica
Cuando las barras del histograma tienen una forma similar a una campana y los valores se agrupan alrededor del centro, se dice que la distribución es normal o simétrica. Este tipo de forma es común en fenómenos naturales, como la estatura o el peso de una población.
Distribución asimétrica
Si las barras se concentran más hacia un lado del gráfico, la distribución es asimétrica. Por ejemplo, si hay más datos a la izquierda, el histograma presenta una asimetría positiva, mientras que si están a la derecha, es negativa.
Distribución uniforme o multimodal
Cuando todas las barras tienen alturas similares, los datos se distribuyen de manera uniforme. En cambio, si existen varios picos, el histograma es multimodal, lo que puede indicar la presencia de diferentes grupos dentro del mismo conjunto de datos.
Aplicaciones del histograma en distintos campos
El histograma se usa en una amplia variedad de áreas, ya que facilita el análisis visual y la toma de decisiones.
En la estadística y la investigación
Los estadísticos emplean el histograma para detectar patrones y evaluar la normalidad de los datos. Esta información resulta clave para elegir el tipo de análisis o prueba que se aplicará posteriormente.
En la calidad y la industria
En el ámbito industrial, el histograma ayuda a controlar procesos de producción. Por ejemplo, permite identificar si las variaciones en la fabricación de piezas se mantienen dentro de los límites aceptables. Así, las empresas pueden mejorar su eficiencia y reducir desperdicios.
En la fotografía digital
Incluso en la fotografía, el histograma tiene un papel importante. En este caso, muestra la distribución de los tonos en una imagen, desde los más oscuros hasta los más claros. Analizar este gráfico ayuda a equilibrar la exposición y a mejorar la calidad visual.
Ventajas y limitaciones del histograma
El histograma ofrece múltiples ventajas. Facilita la comprensión de datos complejos, resalta tendencias y ayuda a detectar valores atípicos. Además, permite comparar diferentes conjuntos de datos de manera visual y directa.
Sin embargo, también presenta limitaciones. Por ejemplo, los resultados pueden variar dependiendo del número y tamaño de los intervalos elegidos. Además, el histograma no muestra valores individuales, sino grupos, por lo que puede perderse cierto nivel de detalle.
Conclusión: el histograma como herramienta esencial
En resumen, el histograma es una herramienta poderosa y versátil para analizar datos cuantitativos. Su capacidad para mostrar la distribución de la información lo convierte en un recurso indispensable tanto en la investigación como en la industria.
Además, al combinar claridad visual y precisión, el histograma permite tomar decisiones informadas basadas en evidencias. Comprenderlo no solo mejora la interpretación de datos, sino que también fortalece las habilidades analíticas en cualquier disciplina.
En definitiva, dominar el uso del histograma es fundamental para transformar números en conocimiento útil y aplicable.